Verdeel een lijn in twee gelijke stukken

• Gegeven is:
  • 2 × AC = CD
  • BD = BE

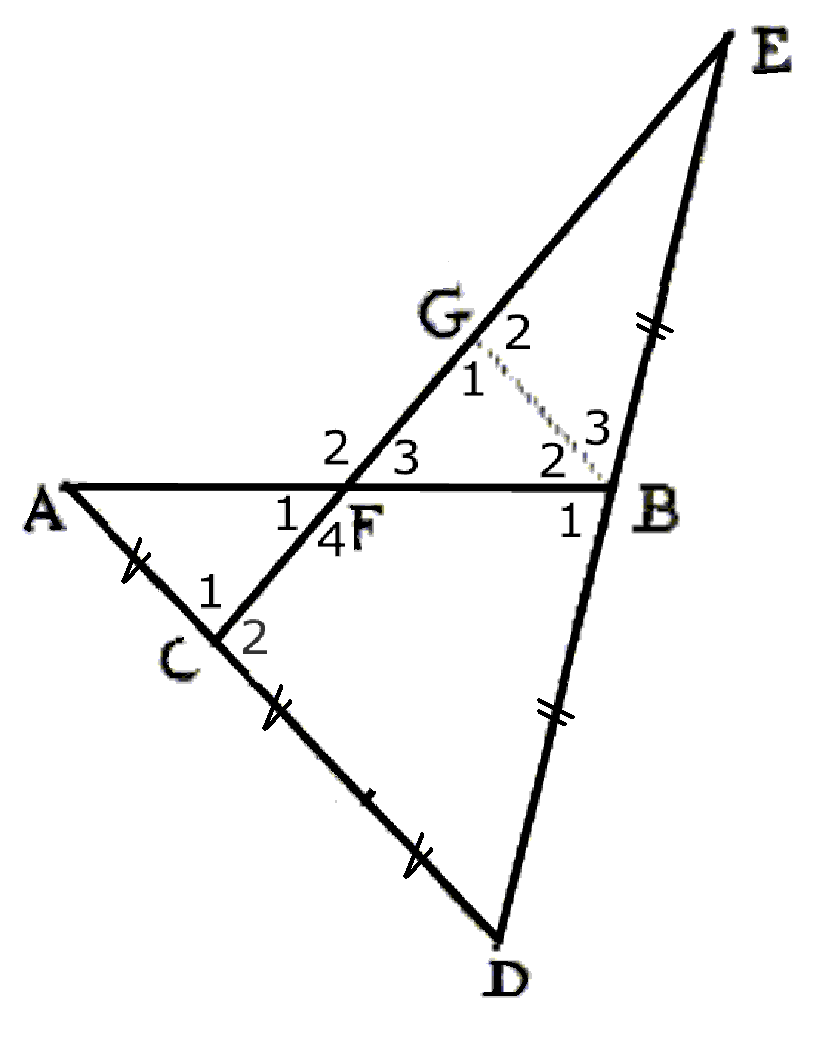
1. Verbind punt B, het midden van DE, met punt G, het midden van lijnstuk CE.
   Lijn BG is een bijzondere lijn.
   Noem enkele bijzondere eigenschappen van deze lijn.
   
   Antwoord: Omdat BD = BE en CG = EG daarom is BG een middenparallel van ∆CDE. Een middenparallel is altijd evenwijdig aan en half zo lang als de zijde van de driehoek die ze niet snijdt. Dus: BG = ½CD = AC (gegeven).
2. Bepaal alle F-hoeken
   
   Antwoord: De lijnen CD en BG zijn evenwijdige lijnen (naar de aard van de constructie) en dus ²⁹ maken snijdende lijnen F-hoeken.
   Lijn EC heeft F-hoeken: ∠G₂ en ∠C₂.
   Lijn ED heeft F-hoeken: ∠B₃ en ∠D.
3. Leg uit waarom ∆CDE een vergroting is van ∆GBE. Bepaal de vergrotingsfactor
   
   Antwoord: Omdat ∆CDE en ∆GBE dezelfde hoek hebben in E en de overeen­komstige hoeken F-hoeken zijn (stap 2) daarom zijn ze gelijkhoekig en dus ^6-4 een vergroting van elkaar.
   De vergrotingsfactor wordt berekend uit de verhouding van de overeen­komstige zijden: BE : DE = 1 : 2.
   De vergrotingsfactor is dus exact 2.
4. Bepaal alle Z-hoeken
   
   Antwoord: De lijnen CD en BG zijn evenwijdige lijnen (naar de aard van de constructie) en dus ²⁹ maken snijdende lijnen Z-hoeken.
   Lijn EC heeft Z-hoeken: ∠C₁ en ∠G₁.
5. Leg uit waarom ∆FCA een vergroting is van ∆FGB.
   Bepaal de vergrotingsfactor.
   
   Omdat ∆FCA en ∆FGB dezelfde hoek hebben in F en de overeen­komstige hoeken Z-hoeken zijn (stap 4) daarom zijn ze gelijkhoekig en dus ^6-4 een vergroting van elkaar.
   Omdat de overeen­komstige zijden BG en AC even lang zijn (stap 1), is de vergrotingsfactor precies één.
6. Verklaar waarom AF = BF.
   
   Antwoord: Omdat ∆ACF = ∆FBG (stap 5), daarom zijn alle overeen­komstige zijden even groot. Dus AF = BF.
7. Leg uit waarom het probleem van de twee boeren is opgelost.
   
   Beide boeren wilden de helft van de weg aanleggen. Ze zochten daarom naar het punt halverwege de weg. Dat is punt F en de gelijke stukken zijn de lijnstukken AF en BF.

Definities

• een middenparallel is een lijnstuk dat de middens van twee zijden van een driehoek met elkaar verbindt.

Proposities van Euclides uit Boek I

29. (Euclides I-29)

Proposities van Euclides uit Boek VI

4. (Euclides VI-4)
5. (Euclides VI-5)