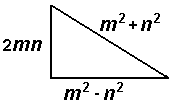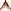Euclides en Pythagoreïsche DrietallenPythagoreïsche drietallen zijn drietallen (a,b,c) met a² + b² = c². Drietallen zijn op verschillende manieren te vinden, bijvoorbeeld door van alles te proberen, met de hand of met hulp van een computer. De oude Babyloniers en de oude Grieken, Pythagoras, Plato en Euclides kenden lang voor de jaartelling bepaalde formules. |
|
Ingeschreven cirkel: loodlijnen
Het middelpunt van de ingeschreven cirkel is het snijpunt van de drie deellijnen. De drie lijnen die loodrecht op de zijden staan en door dat middelpunt gaan, verdelen de zijden in gelijke stukken.
a = x + y en b = x + z en c = y + z
Na substitutie blijkt dat x = ½(a + b − c).
In een rechthoekige driehoek geldt r = x en na substitutie ontstaat
r = ½(m² − n² + 2mn − (m² + n²)) = ½(2mn − 2n²)
Over blijft r = n(m − n)
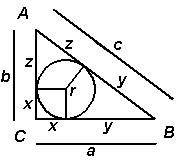
Ingeschreven cirkel: oppervlakte
De oppervlakte O van rechthoekige driehoek ABC kan op twee manieren berekend worden:
- O = ½(a × b)
- O = ½(a × r) + ½(b × r) + ½(c × r) zodat O = r × ½(a + b + c)
- De halve omtrek wordt ook wel de semiperimeter, s, genoemd:
s = ½(a + b + c) = m² + mn = m(m + n) - Hieruit volgt dat
r = a × b = (m² − n²) × (2mn) a + b + c 2m(m + n) - Omdat (m² − n²) = (m + n)(m − n)
kan de vergelijking herschreven worden tot:r = (m + n)(m − n) × (2mn) 2m(m + n) - Deze breuk kan vereenvoudigd worden, zodat r = n(m − n)
Omdat m en n geheeltallig zijn, is het verschil dat ook en het produkt eveneens. Conclusie is dat de straal van een geheeltallige rechthoekige driehoek altijd geheeltallig is.

Euclides boek X propositie 29
Verschillende wiskundigen interpreteren het werk van Euclides op verschillende manieren.
Volgens sommigen voegt Euclides aan zijn formule een vergrotingsfactor k toe en werkt hij met factor ½.
Dan staat er:
a = ½k(m² − n²)
b = kmn
c = ½k(m² + n²)
Viète Opera Mathematica
Frans van Schooten kende het recept van Euclides voor Pythagoreïse drietallen. In 1646 publiceerde hij "Viète Opera Mathematica". Hiernaast zie je een deel van bladzijde 34 met de formules.

 Google Books
Google Books