Mathematische Oeffeningen
Frans van Schooten Junior schreef in zijn "Mathematische Oeffeningen"
over een boekje met landmeetkundige raadsels.
Hij schrijft dat de auteur vermoedelijk een Pools edelman is die in het leger van stadhouder Willem II gediend heeft.
 origineel origineel
Maciej Gloskowski
De auteur van de "Geometria Peregrinans" is een Pools, protestants edelman.
In Polen wordt hij geroemd als dichter, wiskundige cartograaf. Vermoedelijk kwam hij naar de Nederlanden om daar te leren over vestingbouw. Hij beweert aan het hof van Prins Frederik Hendrik te hebben gediend.
 Gloskowski Gloskowski
Geometria Peregrinans
Originelen liggen in universiteitsbibliotheken in Polen.
Dhr Verstraelen heeft de Nederlands vertaling verzorgd.
 vertaling vertaling
|
Raadsel
Een man verstopt in een bos de erfenis voor zijn twee zonen.
Om de schat te vinden geeft hij aanwijzingen.
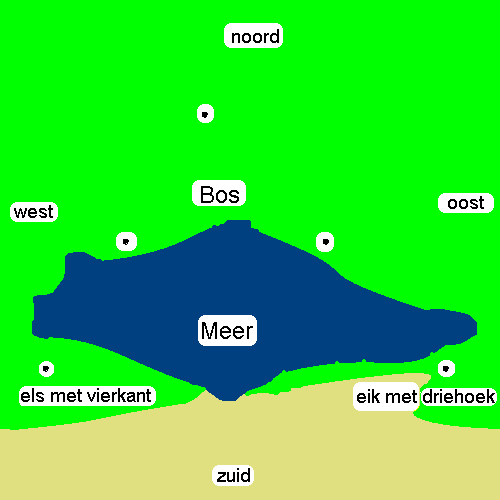
Ga naar het meer en zoek op de westelijke oever een els met daarin een vierkant merkteken.
Aan de andere kant van het meer is een eik met een driehoekig merkteken.
Om de schat te vinden moet je eerst een boom vinden aan de noordzijde.
De afstanden tussen de drie bomen verklapt hij niet, maar hij geeft wel aan hoe de afstanden zich verhouden.
Als de afstand tussen de els en de eik acht eenheden is, dan is die tussen de els en de noordelijke boom zes eenheden
en tussen de eik en de noordelijke boom zeven eenheden.
De ene helft van de schat ligt halverwege de noordelijke boom en de els en de andere helft halverwege de noordelijke boom en de eik.
Het opmeten wordt bemoeilijkt door dat meer, want zoals de schets laat zien, lopen de kijklijnen over dat meer.
Gevraagd wordt om de twee schatten te vinden zonder de afstand tussen eik en els op te meten en zonder mathematische instrumenten te gebruiken.

|
|
 Biografie Biografie
Vader en zoon Frans van Schooten leefden in de 17de eeuw. Zij werkten als docent wiskunde aan de Ingenieursschool in Leiden
 biografie biografie
Raadsels
Frans van Schooten Junior is geinspireerd door de "Geometria Peregrinans".
Gloskowski formuleerde daar een aantal land meetkundige opgaven en beweerde dat deze oplosbaar zijn zonder goniometrie of gradenboog.
 raadsel raadsel
Instrumenten
Het raadsel moet opgelost worden zonder mathematische instrumenten.
Vermoedelijk worden daar hoekmeters als het astrolabium en de Hollandse Cirkel mee bedoeld.
 instrumenten instrumenten
Goniometrie
Met de cosinusregel en een gradenboog laat het probleem zich snel oplossen.
Maar dat is niet de bedoeling.
 goniometrie goniometrie
|
Mathematische Oeffeningen
De "Mathematische Oeffeningen" is een deel van het levenswerk van Frans van Schooten Junior.
Dat werd kort voor zijn dood in 1660 uitgegeven.
Op bladzijde 154 citeert Frans van Schooten de 16 landmeetkundige raadsels uit de "Geometria Peregrinans".
 154
154
-
Hoemen de lengte der liny AB vinden
sal, alsmen tot deselve niet en kan
komen?
-
Hoemen met een voor-gestelde liny,
bepaelt door de baeckens A en B, sonder tot
deselve te komen, in een gegeve wijtte van
deselve, een even-wydige liny trecken sal?
-
Hoemen met een gegeve liny AB, tot
dewelcke men niet komen kan ('tzy dezelve
gesien kan worden of niet,) een parallel-liny van ver trecken sal?
-
Uyt het punt C, 't eeniger plaets buyten de liny AB gegeven (staende
tegen over deselve tussen beyde punten A en B) op deselve AB, sonder
die te genaecken, een perpendiculaer te laten vallen.
-
Hoemen de lengte der hangende, die van een gegeven punt C op een
voorgestelde ongenaeckelijcke liny AB te vallen komt, vinden sal?
-
Hoemen van een punt buyten een voorgestelde liny, 'twelck naer het
zynde der liny gegeven zy, een perpendiculaer van ver op deselve
neerlaten sal?
-
Tot het eynde van een voorgegeve ongenaeckelijcke liny een perpendiculaer
op deselve te laten vallen, soo lang als een begeerde.
-
Van een punt, wijt buyten een voorgestelde liny AB gegeven, op
deselve AB een perpendiculaer te laten vallen, welcke 3 of 4 mael
korter zy.
-
Op een gegeve liny AB ('tzy deselve gesien kan worden of niet) een
gelijck-sydige en rechthoeckige vierhoeck of yets anders dat begeert wort te
maecken, als gestelt wort, datmen tot AB niet komen kan.
-
Gegeven zijnde in een voorgestelde liny of wal des vyandts eenige kenbare
plaets, als mede een seeckere wijtte, waer uyt men een stuck geschuts in een
rechten hoeck tot de gestelde plaets richten moet, de plaets te vinden,
alwaer het stuck gestelt moet worden.
-
Buyten een gegeve liny of deel eens muers, door de punten A en B bepaelt,
in een aengewesen wijtte van desleve door eenich overstaendt punt een plaets
te vinden even-ver van A en B af-gelegen
-
Hoemen buyten de onghenaeckelijcke liny of muer AB een punt vinden sal,
het welck van de punten A en B in een gegeve ongelijcke wijtte volkomen
af-gelegen zy?
-
Het selve in't bosch, alwaer de punten A en B van ver niet gesien konnen
worden, konstichlijck te verrichten.
-
Hoemen uyt het punt C, op d'overstaende liny AB, wanneer men deselve van
C door eenich perijckel of beletsel niet meerder dan den vierde of achtste
part der gantse distantie naerderen kan, een perpendiculaer sal laten
vallen?
-
Het selve op een ander manier, sonder meer als een gegeven getal van
roeden van C naer AB toe te gaen, gevoechlijck te verrichten.
-
Hoe men, 't punt C op de kant van een meyr of bosch gegeven zijnde, ofte
eenich Leger van achter te na by wesende, sonder van C terugh te gaen, en de
muer AB meer als een gegeven getal van roeden van C te naerderen, uyt C op
deselve AB een hangende bequamelijck trecken sal?

Maciej Gloskowski
Navraag bij Poolse universiteitsbibliotheken leidt naar een Pools wiskundige, Maciej Gloskowski, die in de jonge Republiek is geweest en ondermeer wiskunde onderwezen heeft aan de jonge Willem II. Stadhouder Willem II is geboren in 1626 als zoon van Prins Frederik Hendrik. Zijn oom is Prins Maurits. Hij volgt zijn vader op in 1647 en overlijd in 1650 aan een ziekte.
Aan een vertaling van de Poolse biografie wordt gewerkt.
Vertaling
De "Geometria Peregrinans" is geschreven in het Latijn.
Dhr Verstraelen heeft de Nederlands vertaling verzorgd.
Aan de volledige vertaling wordt nog gewerkt.
Er was in de Nederlanden een zekere brave man
die mij vanwege zijn deugd en de studie van de wiskunde mij bijzonder dierbaar was.
Hij was de vader van twee zonen die hij in dezelfde studies had laten onderrichten, voorzover dat gezien hun leeftijd mogelijk was,
maar toen zijn krachten begonnen af te nemen, bedacht hij iets nieuws, opdat zijn zonen die hem zouden overleven,
als hem later wat overkomen was, zich des te enthousiaster op hun eenmaal begonnen studies zouden toeleggen.
Want het beetje geld dat hij had waaruit heel zijn spaargeld bestond deelde hij in tweeën,
nadat hij een klein deel bij een vriend ten behoeve van zijn zonen had achtergelaten.
En hij verborg dat in een bos in de buurt op een bijzonder listige manier.
Uiteindelijk werd hij ziek.
Het was een ziekte die hemzelf later fataal zou worden.
Nadat hij dan zijn zonen bij zich geroepen had en zijn vriend had laten komen, vertrouwde hij de zorg voor hen aan hem toe
en in diens aanwezigheid spoorde hij henzelf als volgt aan:
"Jullie weten", zei hij, "dat mijn ouders mij geen erfenis hebben nagelaten.
Maar wat ik toevallig gehad heb, dat heb ik allemaal gekregen door mijn ijver en handigheid.
Daarom zou het niet onbillijk zijn dat ook jullie door leermeesteres armoede tot dezelfde inspanningen en studie in de deugd zouden aangespoord worden:
omdat het mij wel duidelijk is dat welvaart de zonen van rijke mensen na de dood van hun ouders meestal te gronde gericht heeft.
Opdat toch niet na mijn heengaan jullie de prikkel ontbreekt om de schone kunsten en wetenschappen grondig te leren,
wil ik dat jullie goed weten dat ik al mijn geld, hoe weinig dat ook was in tweeën gedeeld heb
en dat eveneens op twee plaatsen in een naburig bos begraven heb.
Opdat echter jullie zullen kunnen beschikken over dat geld, zij dět voor jullie een aanwijzing:
Jullie weten dat aan de zuidelijke rand van het bos een meer ligt waarvan hetzelfde bos ergens een gedeelte afsluit.
Nu bij de oostelijke oever zullen jullie, nadat jullie het bos zijn ingegaan,
een eik vinden waarin de figuur van een driehoek gesneden is,
maar aan de overkant op de westelijke oever van het meer zal gezocht moeten worden naar een
hoge els waarin het teken van een vierkant is gehakt.
De onderlinge afstand tussen deze bomen is mijzelf, vanwege het tussenliggende meer, niet bekend.
Toch als jullie aan de noordelijke kant van het meer nog in het bos zelf
een punt zullen vinden dat nu juist van de figuur van het vierkant, 6,
maar van het teken van de driehoek, 7 eenheden verwijderd is zodanig als de hele afstand van de figuren zelf 8 eenheden is,
zullen jullie het middelpunt van jullie fortuin vinden.
Van dat punt zullen jullie dus zowel naar de figuur van de driehoek als naar die van het vierkant rechte lijnen trekken,
die zullen lopen over het meer zelf en halverwege de lijnen ligt het verborgen geld.
Maar opdat de luiheid van de een niet de handigheid van de slimste in de weg zal staan; als de een van jullie handigheid te kort komt,
is het de ander geoorloofd beide geldsommen te zoeken en als hij ze gevonden heeft niet meer dan het vierde deel aan de luiste uit te keren.
En toch zal het niet geoorloofd zijn sneller,
of op een andere manier over te gaan tot het zoeken van de erfenis dan dat de knapste in tegenwoordigheid van de andere broer en bovendien van twee vrienden de zaak ten einde zal brengen:
toch zal dit niet uitgevoerd mogen worden met mathematische instrumenten maar alleen met stokken voor dit doel gemaakt;
aangezien de door instrumenten tot stand gekomen afmetingen eerder aan de handigheid dan aan het talent van de makers toegekend moeten worden.
Maar als geen van beiden succes heeft, moet dat geld onaangetast blijven liggen voor diegene van hun nakomelingen
die door zijn aanleg en vaardigheid geschikter bevonden zal worden om dat geld te vinden".
Nadat hij dit uitgesproken had en aan beide zonen de akte overhandigd had die zijn wil kenbaar maakte,
namen zijn krachten geleidelijk af en sloot hij zijn laatste dag af.
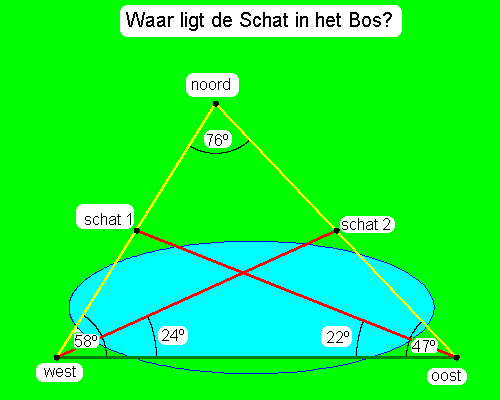
Oplossen met sinusregel en cosinusregel
De hoeken tussen de drie bomen kunnen uitgerekend worden met de cosinusregel.
Vervolgens kunnen met de sinusregel de hoeken naar de punten halverwege uitgerekend worden.
Na deze rekenexercitie kunnen met een hoekmeter de kijklijnen worden uitgezet.
De schat ligt dan op de kruising van die kijklijnen.
Opdracht is echter om het zonder de hoekmeter te doen.
 www.fransvanschooten.nl
www.fransvanschooten.nl










