Law of Tangents
|
In addition to the well-known law of sines and law of cosines, there is also the law of tangents. The first two laws are in your math textbook, but you won't find the latter anymore. This article brings out the law of tangent again and shows you, among other things, when it is very useful.
The tangent rule is an example of a rule that came and went. In the seventeenth century the tangent rule was proved with geometry, in the nineteenth century with trigonometric relationships, and sometime in the twentieth century the tangent rule was dropped from textbooks.
This article first explains what the tangent rule is and how to use it. Next comes the seventeenth-century geometric proof. Next, the trigonometric relations are discussed. Finally, we let Professor Van der Waerden talk about how useful it is to memorize all these rules.
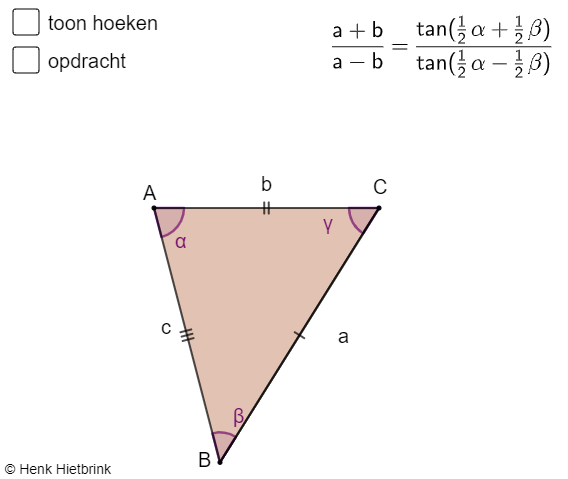
Law of Sines, Law of Cosines and Law of TangentsIn any triangle ABC with vertices A, B and C, sides a, b and c and angles α, β and γ, the law of sines, the law of cosines and the law of tangents apply. You probably know the first two:
and
The law of sines has a nice rhythm, the law of cosines is somewhat like Pythagoras' theorem, but the law of tangents has a different form and is less well known:
If you want to memorize the formula, focus on sum and difference: the tangent of the half sum is to the tangent of the half difference as the sum is to the difference. Choose the appropriate ruleMathematics requires the skills to quickly choose the right formula in any situation. Each of the three rules has a specific application. Below are some situations. The question is which of the three rules is best to use. Exercise 1Given sides a and b and angle α, which rule do you use to calculate side c and angle β and γ? Exercise 2Given sides b and c and angle α, which rule do you use to calculate side a? Exercise 3Given sides a, b and c, which rule do you use to calculate angle α, β and γ? Exercise 4Given sides a and b and angle γ, which rule do you use to calculate angle α and β? | ||||||||||||||||||||||||||||||||||
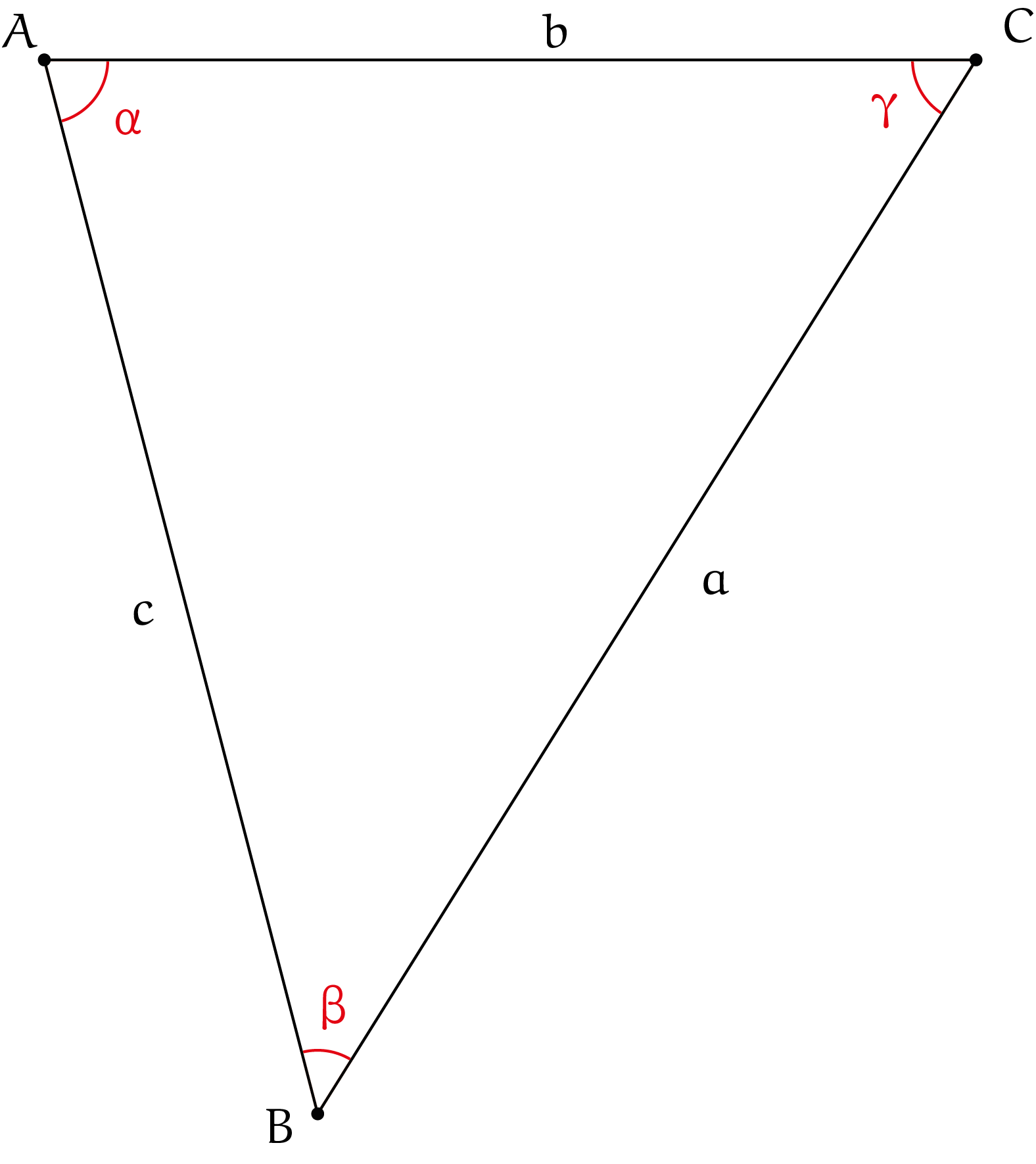
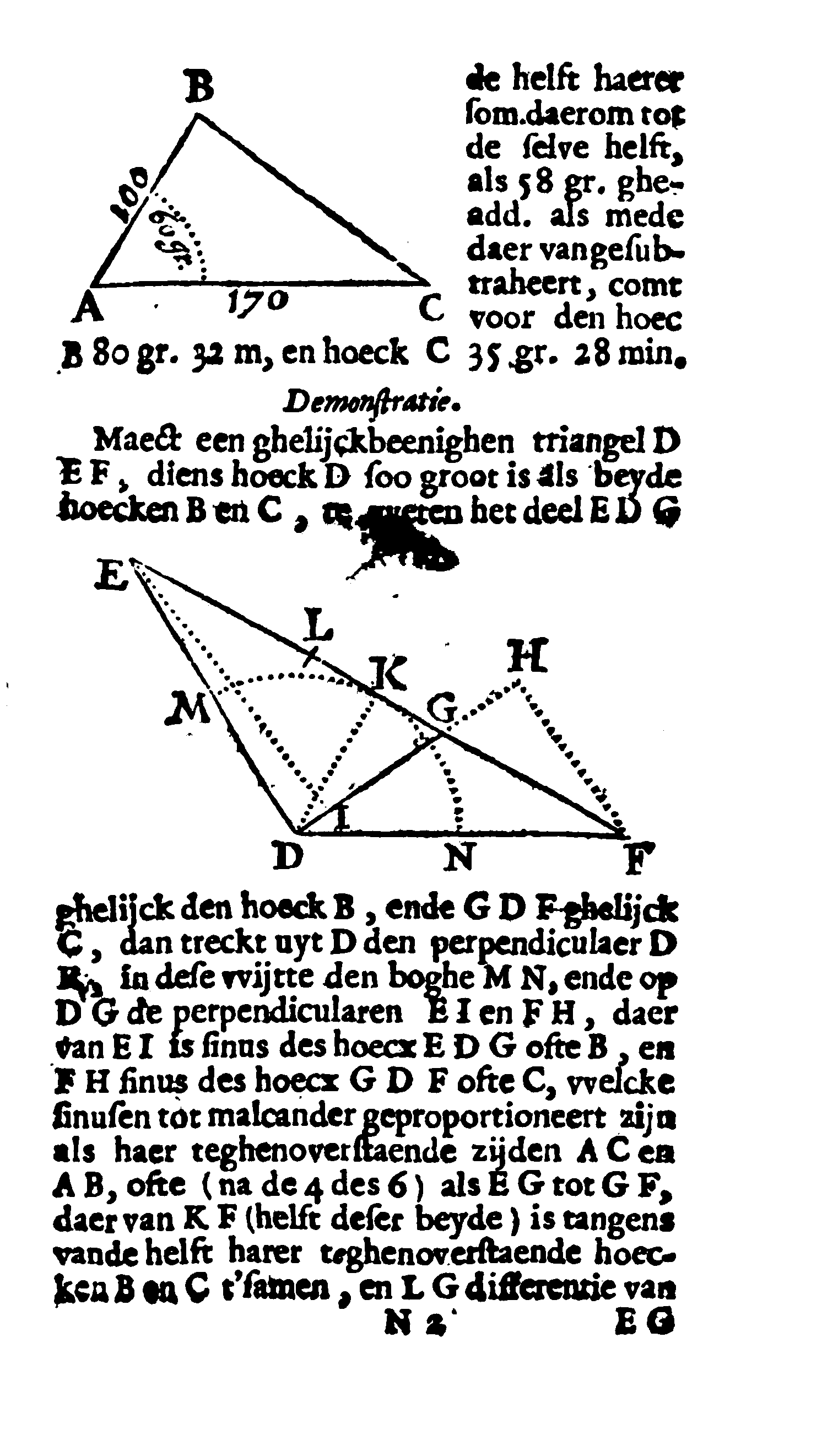
ApplicationIf you do not know the law of tangents, you will first apply the law of cosines to calculate the length of side c in exercise 4, and then the law of sines for the angles α and β. This can be done in a shorter way with the law of tangents. You may think that you cannot calculate the tangent in the numerator and denominator, but remember that if the magnitude of angle γ is given, then the sum of angles α + β is also known, because α + β = 180° − γ. So you can calculate the tangent in the numerator! In short, the tangent rule is very efficient when you only want to know the unknown angles α and β. If you want to figure out the calculation scheme yourself, you can get started with the triangle ABC with a = BC = 4, b = AC = 3 and γ = ∠ACB = 58°. Calculation schemeLater you will do some math, but it is always useful to make a drawing first to estimate the order of magnitude. Draw the above triangle ABC with a = 4, b = 3 and γ = 58° with pencil on paper or with GeoGebra.Exercise 5Draw this triangle and measure the magnitude of the angles α and β. Exercise 6Also measure the length of side AB. Below is a calculation scheme based on a page from an anonymous manuscript from the 17th century in the possession of Forum Rare Books. The tangent rule reads:
The anonymous author makes the following steps. First calculate sum and difference: a + b = 7 and a − b = 1. Then sum the angles α + β = 180°−58° = 122° so that α + β = 61° with tan(½(α + β)) ≈ 1.8040. You have now computed three of the four parts of the law of tangents and can therefore calculate the unknown tangent of the half difference: tan(½(α − β)) ≈ 0.2577. so that α − β ≈ 14.45°. Finally, α = (α + β) + (α − β) ≈ 74.45° and β = (α + β) − (α − β) ≈ 46.55°. Exercise 7Calculate the entire math chart yourself and check your answers with your drawing. ProofsThe nice thing about mathematics is that you can prove any rule, including the tangent rule. On WisFaq and Wikipedia there are proofs that use Simpson's rules about the sum or difference of two angles. You usually don't get these rules until exam year. Those proofs do not use two line segments of length a+b and a−b. In this article, we discuss a geometric proof where those line segments do appear in the drawing. You can follow this proof if you have learned geometric reasoning and know the trigonometry of the right-angled triangle.Example from the manuscriptThe figure shows a page from that 17th century manuscript. You see the triangle and all the calculations. Given is triangle ABC with BC = 66, AB = 105 and
Exercise 8Using the law of tangents, calculate the magnitude of the angles at points A and C. Notice that the lettering of the points is different from the previous problem. Given are a, c and β. In this situation you can rewrite the law of tangents as:
Completion gives
Rounded to two decimal places, γ − α ≈ 22.86° so that
| ||||||||||||||||||||||||||||||||||
Geometrical ProofIn the drawing of the manuscript from the 17th century, guide lines are drawn. Those guide lines construct two isosceles triangles. Unfortunately, in the manuscript the points are not so conveniently chosen for our purpose. Therefore, we return to figure 3 of triangle ABC with given sides a, b and angle γ. Conveniently a > b so α > β. We start with an auxiliary line. We extend line segment AC to point D with BC = CD so that the length of AD equals a + b. Thus triangle BCD is isosceles. Exercise 9Express the angles of triangle BCD in γ. | ||||||||||||||||||||||||||||||||||
|
Line segment AOE is the second auxiliary line with AC=CO, making BO = a − b. Thus triangle ACO is also isosceles. Exercise 10Express the angles of triangle ACO in α and β. Thanks to these two auxiliary lines, line segments are construct with length a + b and a − b, two angles of size ½γ and two angles of size α + β. First you are going to show that ∠E is a right angle, then you are going to look for expressions for tan(½(α + β)) and tan(½(α − β)). | ||||||||||||||||||||||||||||||||||
Exercise 11Explore triangle BEO and prove ∠E = 90°. Also, verify in Figure 4 how large ∠AOC is. Exercise 12
Exercise 13
The triangles BEO and DEA are similar because of that equal right angle and that equal base angle γ such that
Due
Finally, the requested follows, namely the tangent rule:
| ||||||||||||||||||||||||||||||||||
HistoryShortly before 1600, mathematicians were looking for new trigonometric relationships. Slowly but surely, they came up with new expressions. Latin was then the scientific language. Eventually Viète gives the tangent rule in words, but it is quite a feat to recognize the modern expression in the sentence below. To begin with, you should know that there was no word for tangent yet. Viète talks about the prosine on page 402! Around 1900, the focus shifted from geometry to algebra. The proof of the tangent rule shifted to applying trigonometric rules like the sum and difference rule. Pay attention to the plus and minus signs.
sin(α) + sin(β) = 2·sin(½(α + β)) · cos(½(α − β))
sin(α) − sin(β) = 2·sin(½(α − β)) · cos(½(α + β)) Exercise 14Show that you can reduce the expression
Exercise 15Apply the sum and difference rule to prove the tangent rule. | ||||||||||||||||||||||||||||||||||
Could it be simpler?In 1930, Van der Waerden wondered why textbooks focused on the tangent rule and that trigonometric proof. His position was that students learn mathematics by thinking about trivial auxiliary lines like the contour line. Try for yourself. Exercise 16Return to the task about triangle ABC with a = BC = 4, b = AC = 3 and γ = ∠ACB = 58°. Draw the altitude line from point A with base point V on side BC.
Exercise 17Now show that
| ||||||||||||||||||||||||||||||||||
ConclusionThe law of tangents is a logical addition to the law of sines and the law of cosines. The nice thing is that a century old manuscript provided clarity about the geometric reasoning behind the tangent rule. You have discovered that there are elegant, rhythmic formulas, but you've also seen that altitude lines and the trigonometry of the right-angled triangle get you just as far. |
Tabulae sinuum tangentium secantium, ad radium 10 000 000
In 1627, Frans van Schooten Sr published a handy table book of rules, examples and proofs. Long titles were common then. The full title is "Tabulae sinuum tangentium secantium, ad radium 10 000 000; met 't gebruyck der selve in rechtlinische Triangulen".
GeoGebra
My animation shows how the auxiliary lines were chosen.
Literatuur
- Frans van Schooten, (1646), Vietae opera mathematica, Leiden, Elsevier
 ETH rara
ETH rara
- Van der Waerden, (1930), de tangensregel in de goniometrie, in: Euclides, 6e jaargang 1930, Nr. 5-6,
Groningen, Noordhoff
 Archief Vakblad Euclides
Archief Vakblad Euclides






-Portrait-Portr_12193.tif.jpg)
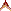


 larger version including zoom
larger version including zoom
 Dutch
Dutch