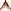Vestingbouw

Grontteyckening

Op bladzijde 11 herhaalt Stevin wat hij op bladzijde 8 begonnen is. Op bladzijde 8 staan de maten van de zeshoekige vesting, en op bladzijde 11 staat hoe deze afmetingen op papier getekend kunnen worden. Op bladzijde 8 staat bijvoorbeeld het principe "Ten 3en, de breede des strijckhoucx {Flanc.} opde voorsijde des tants vande middelplaets, met de dickte des schutsels {Oreillon.}, t'samen 140 voeten." en op bladzijde 11 staat de instructie "Ten 3en, om te hebben de breede des strijckhoucks {Flanc.}, met de dickte van haer schutsel {Oreillon.} soo treck ick HM lanck 140 voeten, ende rechthouckich op BC. Inder selver voughen treck ick IN rechthouckich op BG, ende KO rechthouckich op CB, doende der ghelijcke op al dander der ghelijcke plaetsen."

maten bij de grontteyckening
 

De animatie toont nauwgezet de stappen die Stevin zet bij de construeren van de tekening. De tekening is uitgedrukt in Rijnlandse roeden (3,767 meter). De animatie toont afstanden in roeden en in meters.
Opvallend is hoe zorgvuldig de houtsnede is gemaakt. Alle lijnen en punten liggen goed op hun plaats.

grote versie geogebra applet inclusief zoom

Google Books: Sterctenbovwing, bladzijde 18

Verheven Teyckening

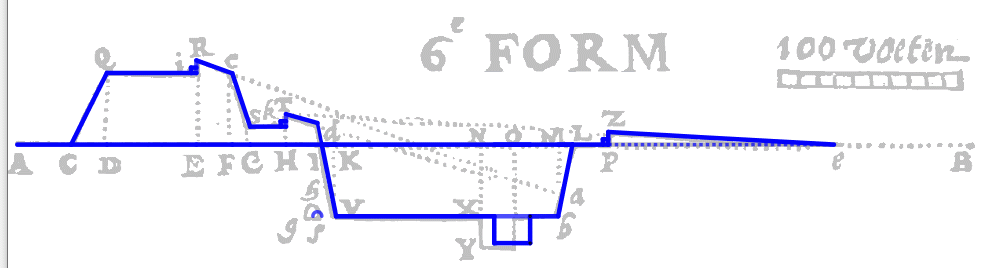
Op bladzijde 22 geeft Stevin de maten van de verschillende onderdelen van een zeshoekige vesting. Op bladzijde 23 geeft hij aan hoe alles in een tekening gezet kan worden.

maten bij de verheven teyckening
 

De animatie toont nauwgezet de stappen die Stevin zet bij de construeren van de tekening. De tekening is uitgedrukt in Rijnlandse voeten (31,39 cm). De animatie toont lengte, breedte en hoogte in voeten en in meters. Ook deze houtsnede is accuraat gemaakt, want bijna alle lijnen en punten liggen perfect op hun plaats. Alleen de punten N en O, die de ligging van de verdiepte middelgracht markeren zijn niet juist aangegeven.
Pas wanneer voeten omgerekend worden naar meters valt op hoe hoog Stevin's vesting is (stap 13) en hoe diep de gracht (stap 18) is. Het is onwaarschijnlijk dat een hoogte en diepte van tien of meer meter in de zeventiende eeuw gerealiseerd konden worden in de slappe Hollandse veengronden met zijn hoge grondwaterstanden. Na 1600 verschijnen er in Nederland veel boeken over vestingbouw. De voorgestelde vesting is dan nog maar enkele meters hoog en de gracht slechts twee meter diep. Het ontwerp van Stevin met wallen van 12 meter hoog en grachten van 17 meter diep past eerder bij de terreingesteldheid van Vlaanderen, Brabant en Henegouwen.

grote versie geogebra applet inclusief zoom

Google Books: Sterctenbovwing, bladzijde 25

Vergelijking van vestingen

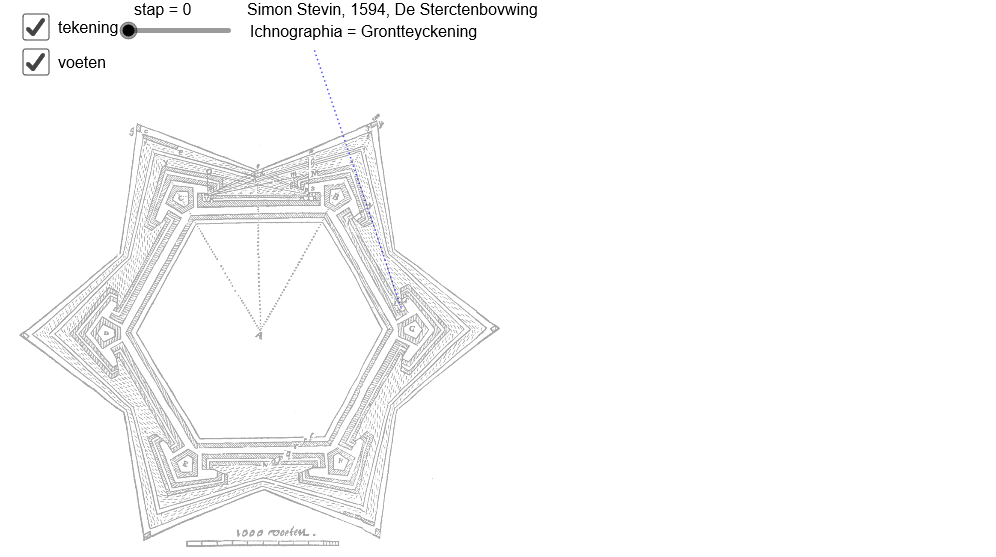
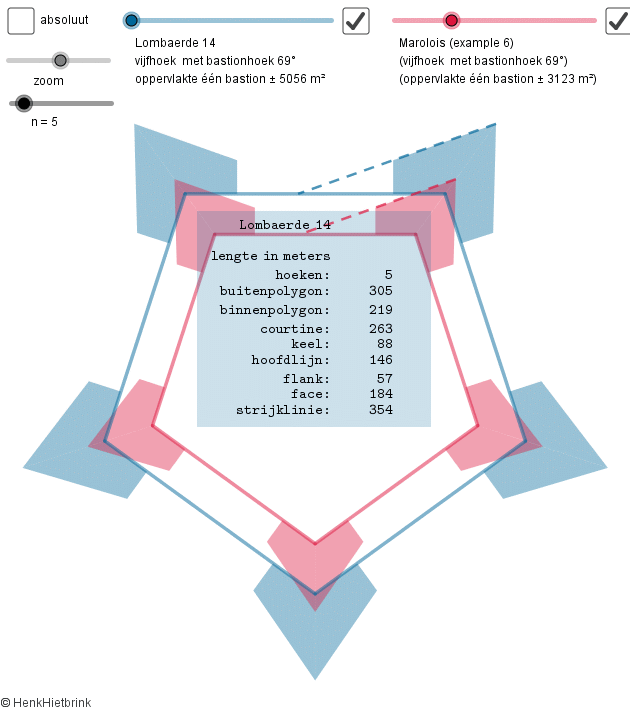
In de zeventiende eeuw verscheen een groot aantal boeken over vestingbouw. Ieder zich zelf respecterende schrijver had een eigen systeem om aan de afmetingen van een vesting te rekenen. Waar de ene auteur werkte met alleen rechthoekige driehoeken, liet de ander zien dat hij de sinusregel beheerste of zelfs de tangensregel. Ook koos iedere auteur voor eigen uitgangspunten met iets andere hoeken en lengtes aardoor iedere vesting er net iets anders uitzag.

In Geogebra is een animatie gemaakt dat een overzicht geeft van de voorstellen van een groot aantal auteurs, van Simon Stevin tot Abraham de Graaf. Zo kunnen de verschillende ontwerpen met elkaar vergeleken worden.

grote versie geogebra applet inclusief zoom

Vergelijking van bolwerken

In Geogebra is een animatie gemaakt dat een overzicht geeft van de verschillen in de grootte van de bolwerken: bolwerkhoek, keel, flank, face en hoofdlijn. Zo kunnen de verschillende ontwerpen met elkaar vergeleken worden.

grote versie geogebra applet inclusief zoom

Teken je eigen vesting in GeoGebra

In Geogebra is een animatie gemaakt waarmee je zelf een eigen vesting kunt tekenen. Je kunt kiezen hoeveel zijden de veelhoek heeft en zo een zeshoek, zevenhoek of twaalfhoek maken. Je kunt zelf de lengte kiezen van bijvoorbeeld de zijde, de keel, de courtine en de hoofdlijn of face. Ook kun je de grootte van de flankhoek instellen.

grote versie geogebra applet inclusief zoom

Quiz