XV met sloot

Van een vierhoekig stuk land ABCD zijn op zijde AD de punten E, F, G, D en H bepaald.
Lijn BE maakt een rechte hoek met zijde AD.
Op lijn BG ligt punt C.
Ook lijn CF maakt een rechte hoek met zijde AD.
Lijn HI verdeelt vierhoek ABCD in twee even grote delen. Lijn HI maakt ook een rechte hoek met zijde DC.
Enkele afmetingen zijn bekend: AE = 13, EF = 9, FG = 5 en GD = 8

In de buurt van scheidslijn HI komt een sloot KLMN van één roede breed die de vierhoek ABCD verdeelt in twee even grote stukken ABLK en NMCD. Bereken de lengte AK.

Lengtes werden in de zeventiende eeuw werkte niet uitgedrukt in meters of kilometers maar in roeden en voeten. Een roede en een voet zijn lengtematen. De Rijnlandse roede is ongeveer 3,77 meter. Twaalf voeten gaan in één roede.

tip    tip 1.  Gebruik HG = 13 (zie bladzijde 63)   2. Stel KN = 2×b en OH = x zodat KO = ON = b en KH = b − x en HN = b + x. antwoord    antwoord Doel is dat opp. KLIH = opp. HIMN. Gegeven is HG = 13 (zie bladzijde 63) Stel KN = 2×b en OH = x zodat KO = ON = b en KH = b − x en HN = b + x. opp. KLIH : opp. HIMN = ½ (KL + IH) (b − x) : (IH + MN) (b + x) = 1 : 1 (KG + HG) (b − x) : (HG + NG) (b + x) = 1 : 1 ((HG + b − x) + HG) (b − x) = (HG + (HG − b − x)) (b + x) x = √ HG² − b² In het geval dat HG = 13 en dat de sloot één roede breed is, KN = 1, is b = 0,5 en is x ≈ 0,01, zodat AK = AE + EH − b + x ≈ 13,51. Zoals je ziet, Frans van Schooten Jr is accuraat en precies: de sloot wordt op een honderdste van die ene roede breedt bepaald. 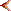opdracht 15 opdracht 17